常用12大排序算法之十：桶排序算法-基数排序算法

2017-04-22 23:32 阅读 4,550 次 评论 0 条

1.桶排序的基本思想

桶排序的基本思想是将一个数据表分割成许多buckets，然后每个bucket各自排序，或用不同的排序算法，或者递归的使用bucket sort算法。也是典型的divide-and-conquer分而治之的策略。它是一个分布式的排序，介于MSD基数排序和LSD基数排序之间。

桶排序算法要求，数据的长度必须完全一样，程序过程要产生长度相同的数据

关于基数排序，可以参考《常用12大排序算法之九：基数排序(LSD+MSD)-桶子法排序》。

 

2.桶排序的基本流程

（1）具体过程

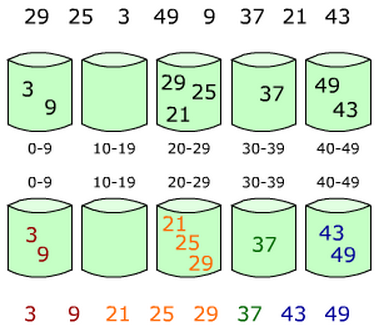
建立一堆buckets；

遍历原始数组，并将数据放入到各自的buckets当中；

对非空的buckets进行排序；

按照顺序遍历这些buckets并放回到原始数组中即可构成排序后的数组。

桶排序

（2）代码实现过程

设置一个定量的数组当作空桶子；

寻访序列，并且把项目一个一个放到对应的桶子去；

对每个不是空的桶子进行排序；

从不是空的桶子里把项目再放回原来的序列中。

 

3.桶排序的复杂度

桶排序利用函数的映射关系，减少了几乎所有的比较工作。实际上，桶排序的f(k)值的计算，其作用就相当于快排中划分，已经把大量数据分割成了基本有序的数据块(桶)。然后只需要对桶中的少量数据做先进的比较排序即可。

对N个关键字进行桶排序的时间复杂度分为两个部分：

(1) 循环计算每个关键字的桶映射函数，这个时间复杂度是O(N)。

(2) 利用先进的比较排序算法对每个桶内的所有数据进行排序，其时间复杂度为 ∑ O(Ni*logNi) ,其中Ni 为第i个桶的数据量。

很显然，第(2)部分是桶排序性能好坏的决定因素。尽量减少桶内数据的数量是提高效率的唯一办法(因为基于比较排序的最好平均时间复杂度只能达到O(N*logN)了)。因此，我们需要尽量做到下面两点：

(1) 映射函数f(k)能够将N个数据平均的分配到M个桶中，这样每个桶就有[N/M]个数据量。

(2) 尽量的增大桶的数量。极限情况下每个桶只能得到一个数据，这样就完全避开了桶内数据的“比较”排序操作。 当然，做到这一点很不容易，数据量巨大的情况下，f(k)函数会使得桶集合的数量巨大，空间浪费严重。这就是一个时间代价和空间代价的权衡问题了。

对于N个待排数据，M个桶，平均每个桶[N/M]个数据的桶排序平均时间复杂度为：

O(N)+O(M*(N/M)*log(N/M))=O(N+N*(logN-logM))=O(N+N*logN-N*logM)

当N=M时，即极限情况下每个桶只有一个数据时。桶排序的最好效率能够达到O(N)。

总结：桶排序的平均时间复杂度为线性的O(N+C)，其中C=N*(logN-logM)。如果相对于同样的N，桶数量M越大，其效率越高，最好的时间复杂度达到O(N)。当然桶排序的空间复杂度为O(N+M)，如果输入数据非常庞大，而桶的数量也非常多，则空间代价无疑是昂贵的。此外，桶排序是稳定的。

 

4.桶排序算法C语言源代码

桶排序算法C语言源代码
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
/**
* 算法君：一个专业的算法学习分享网站
* 算法君：专业分享--数据剖析--算法精解
* 算法君：http://www.suanfajun.com
*/
 
 
#include<stdio.h>
 
#define Max_len 10      //数组元素个数
 
// 打印结果
void Show(int  arr[], int n)
{
    int i;
    for ( i=0; i<n; i++ )
        printf("%d  ", arr[i]);
    printf("\n");
}
 
//获得未排序数组中最大的一个元素值
int GetMaxVal(int* arr, int len)
{
    
    int maxVal = arr[0]; //假设最大为arr[0]
    
    for(int i = 1; i < len; i++)  //遍历比较，找到大的就赋值给maxVal
    {
        if(arr[i] > maxVal)
            maxVal = arr[i];
    }
    
    return maxVal;  //返回最大值
}
 
//桶排序   参数：数组及其长度
void BucketSort(int* arr , int len)
{
    int tmpArrLen = GetMaxVal(arr , len) + 1;
    int tmpArr[tmpArrLen];  //获得空桶大小
    int i, j;
    
    for( i = 0; i < tmpArrLen; i++)  //空桶初始化
        tmpArr[i] = 0;
    
    for(i = 0; i < len; i++)   //寻访序列，并且把项目一个一个放到对应的桶子去。
        tmpArr[ arr[i] ]++;
    
    for(i = 0, j = 0; i < tmpArrLen; i ++)
    {
        while( tmpArr[ i ] != 0) //对每个不是空的桶子进行排序。
        {
            arr[j ] = i;  //从不是空的桶子里把项目再放回原来的序列中。
            j++;
            tmpArr[i]--;
        }
    }
}
 
int main()
{   //测试数据
    int arr_test[Max_len] = { 8, 4, 2, 3, 5, 1, 6, 9, 0, 7 };
    
    //排序前数组序列
    Show( arr_test, Max_len );
    //排序
    BucketSort( arr_test,  Max_len);
    //排序后数组序列
    Show( arr_test, Max_len );
    
    return 0;
}

 

5.桶排序算法C++源代码

桶排序算法C++源代码
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
/**
* 算法君：一个专业的算法学习分享网站
* 算法君：专业分享--数据剖析--算法精解
* 算法君：http://www.suanfajun.com
*/
 
 
#include<iostream>
#include<vector>
using namespace std;
class A{
public:
    int length;
    vector<int> a;
};
void insertSort(vector<int> &b){
    int size = b.size();
    int key,i;
    for(int j=1;j<size;j++){
        key=b[j];
        i=j-1;
        while(i>=0&&b[i]>key){
            b[i+1]=b[i];
            i=i-1;
        }
        b[i+1]=key;
    }
}
void bucketSort(A &array){
    int n = array.length;
    vector<vector<int>> b;
    for(int i=0;i<array.length;i++){
        vector<int> tmp;
        b.push_back(tmp);
    }
    for(int i=0;i<array.length;i++){
        int tmp = array.a[i];
        if(array.a[i]/10==0)
            b[0].push_back(tmp);
        if(array.a[i]/10==1)
            b[1].push_back(tmp);
        if(array.a[i]/10==2)
            b[2].push_back(tmp);
        if(array.a[i]/10==3)
            b[3].push_back(tmp);
        if(array.a[i]/10==4)
            b[4].push_back(tmp);
        if(array.a[i]/10==5)
            b[5].push_back(tmp);
        if(array.a[i]/10==6)
            b[6].push_back(tmp);
        if(array.a[i]/10==7)
            b[7].push_back(tmp);
        if(array.a[i]/10==8)
            b[8].push_back(tmp);
        if(array.a[i]/10==9)
            b[9].push_back(tmp);
    }
    for(int i=0;i<10;i++){
        insertSort(b[i]);
    }
    for(vector<vector<int>>::iterator iter=b.begin();iter!=b.end();iter++){
        for(vector<int>::iterator iter2=(*iter).begin();iter2!=(*iter).end();iter2++){
            cout<<*iter2<<endl;
        }
    }
}
int main(){
    A array;
    int m;
    array.length=10;
    array.a.push_back(23);
    array.a.push_back(11);
    array.a.push_back(16);
    array.a.push_back(82);
    array.a.push_back(98);
    array.a.push_back(73);
    array.a.push_back(63);
    array.a.push_back(19);
    array.a.push_back(31);
    array.a.push_back(26);
    bucketSort(array);
    cin>>m;
    return 0;
}

 

 

版权声明：本文著作权归原作者所有，欢迎分享本文，谢谢支持！
转载请注明：常用12大排序算法之十：桶排序算法-基数排序算法 | 算法君
分类：数据结构 标签：,

发表评论


表情