1.堆排序的基础知识
(1)堆分类:
a.最大堆:所有节点的子节点比其自身小的堆。
b.最小堆:所有节点的子节点比其自身大的堆。
(2)堆排序简介
堆分为最大堆和最小堆,其实就是完全二叉树。最大堆要求节点的元素都要大于其孩子,最小堆要求节点元素都小于其左右孩子,两者对左右孩子的大小关系不做任何要求,其实很好理解。
根据上面的定义,我们可以得知,处于最大堆的根节点的元素一定是这个堆中的最大值。其实我们的堆排序算法就是抓住了堆的这一特点,每次都取堆顶的元素,将其放在序列最后面,然后将剩余的元素重新调整为最大堆,依次类推,最终得到排序的序列。
或者说,堆排序将所有的待排序数据分为两部分,无序区和有序区。无序区也就是前面的最大堆数据,有序区是每次将堆顶元素放到最后排列而成的序列。每一次堆排序过程都是有序区元素个数增加,无序区元素个数减少的过程。当无序区元素个数为1时,堆排序就完成了。
本质上讲,堆排序是一种选择排序,每次都选择堆中最大的元素进行排序。只不过堆排序选择元素的方法更为先进,时间复杂度更低,效率更高。
(3)堆排序基本思想
利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性,使得每次从无序中选择最大记录(最小记录)变得简单。其基本思想为(大顶堆):
(1)将初始待排序关键字序列(R1,R2....Rn)构建成大顶堆,此堆为初始的无须区;
(2)将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n];
(3)由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
2.堆排序的步骤
(1)首先从第一个非叶子节点开始,比较当前节点和其孩子节点,将最大的元素放在当前节点,交换当前节点和最大节点元素;
(2)将当前元素前面所有的元素都进行1的过程,这样就生成了最大堆;
(3)将堆顶元素和最后一个元素交换,列表长度减1。由此无序区减1,有序区加1;
(4)剩余元素重新调整建堆;
(5)继续3和4,直到所有元素都完成排序。
3.堆排序举例
给定一个整形数组a[]={16,7,3,20,17,8},对其进行堆排序。
(1)首先根据该数组元素构建一个完全二叉树,得到如下结果:
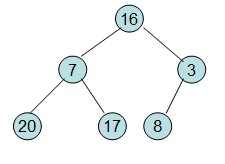
堆排序-1
(2)然后需要构造初始堆,则从最后一个非叶节点开始调整,调整过程如下:
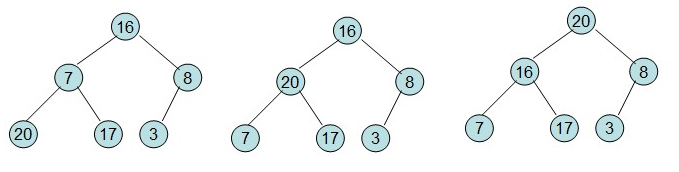
堆排序-2
(3)20和16交换后导致16不满足堆的性质,因此需重新调整,结果如下:
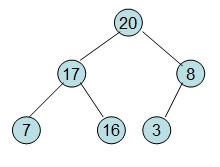
堆排序-3
(4)这样就得到了初始堆:即每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换(交换之后可能造成被交换的孩子节点不满足堆的性质,因此每次交换之后要重新对被交换的孩子节点进行调整)。有了初始堆之后就可以进行排序了。
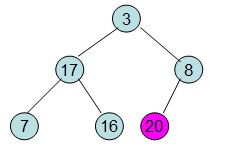
堆排序-4 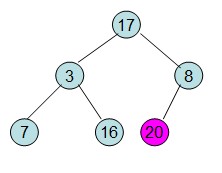 堆排序-5
堆排序-5
(5)此时3位于堆顶不满堆的性质,则需调整继续调整,结果如下:
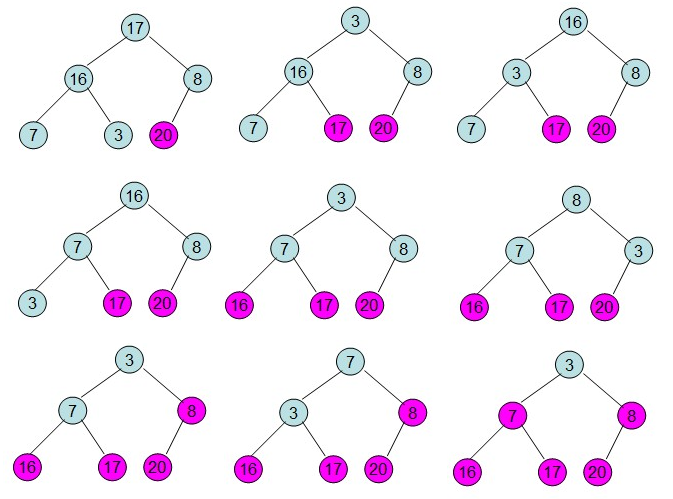
堆排序-6
这样整个区间便已经有序了。
4.堆排序算法分析
从上述过程可知,堆排序其实也是一种选择排序,是一种树形选择排序。只不过直接选择排序中,为了从R[1...n]中选择最大记录,需比较n-1次,然后从R[1...n-2]中选择最大记录需比较n-2次。
事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过,而树形选择排序恰好利用树形的特点保存了部分前面的比较结果,因此可以减少比较次数。
对于n个关键字序列,最坏情况下每个节点需比较log2(n)次,因此其最坏情况下时间复杂度为nlogn。堆排序为不稳定排序,不适合记录较少的排序。
5.堆排序算法C语言源代码
(1)第一种方案:第1部分
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 | /** * 算法君:一个专业的算法学习分享网站 * 算法君:专业分享--数据剖析--算法精解 * 算法君:http://www.suanfajun.com */ // 基于最大堆实现升序排序 // 初始化堆 void initHeap(int a[], int len) { // 从完全二叉树最后一个非子节点开始 // 在数组中第一个元素的索引是0 // 第n个元素的左孩子为2n+1,右孩子为2n+2, // 最后一个非子节点位置在(n - 1) / 2 for (int i = (len - 1) / 2; i >= 0; --i) { adjustMaxHeap(a, len, i); } } void adjustMaxHeap(int a[], int len, int parentNodeIndex) { // 若只有一个元素,那么只能是堆顶元素,也没有必要再排序了 if (len <= 1) { return; } // 记录比父节点大的左孩子或者右孩子的索引 int targetIndex = -1; // 获取左、右孩子的索引 int leftChildIndex = 2 * parentNodeIndex + 1; int rightChildIndex = 2 * parentNodeIndex + 2; // 没有左孩子 if (leftChildIndex >= len) { return; } // 有左孩子,但是没有右孩子 if (rightChildIndex >= len) { targetIndex = leftChildIndex; } // 有左孩子和右孩子 else { // 取左、右孩子两者中最大的一个 targetIndex = a[leftChildIndex] > a[rightChildIndex] ? leftChildIndex : rightChildIndex; } // 只有孩子比父节点的值还要大,才需要交换 if (a[targetIndex] > a[parentNodeIndex]) { int temp = a[targetIndex]; a[targetIndex] = a[parentNodeIndex]; a[parentNodeIndex] = temp; // 交换完成后,有可能会导致a[targetIndex]结点所形成的子树不满足堆的条件, // 若不满足堆的条件,则调整之使之也成为堆 adjustMaxHeap(a, len, targetIndex); } } void heapSort(int a[], int len) { if (len <= 1) { return; } // 初始堆成无序最大堆 initHeap(a, len); for (int i = len - 1; i > 0; --i) { // 将当前堆顶元素与最后一个元素交换,保证这一趟所查找到的堆顶元素与最后一个元素交换 // 注意:这里所说的最后不是a[len - 1],而是每一趟的范围中最后一个元素 // 为什么要加上>0判断?每次不是说堆顶一定是最大值吗?没错,每一趟调整后,堆顶是最大值的 // 但是,由于len的范围不断地缩小,导致某些特殊的序列出现异常 // 比如说,5, 3, 8, 6, 4序列,当调整i=1时,已经调整为3,4,5,6,8序列,已经有序了 // 但是导致了a[i]与a[0]交换,由于变成了4,3,5,6,8反而变成无序了! if (a[0] > a[i]) { int temp = a[0]; a[0] = a[i]; a[i] = temp; } // 范围变成为: // 0...len-1 // 0...len-1-1 // 0...1 // 结束 // 其中,0是堆顶,每次都是找出在指定的范围内比堆顶还大的元素,然后与堆顶元素交换 adjustMaxHeap(a, i - 1, 0); } } |
(1)第一种方案:第2部分
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 | /** * 算法君:一个专业的算法学习分享网站 * 算法君:专业分享--数据剖析--算法精解 * 算法君:http://www.suanfajun.com */ // 基于最小堆实现降序排序 // 初始化堆 void initHeap(int a[], int len) { // 从完全二叉树最后一个非子节点开始 // 在数组中第一个元素的索引是0 // 第n个元素的左孩子为2n+1,右孩子为2n+2, // 最后一个非子节点位置在(n - 1) / 2 for (int i = (len - 1) / 2; i >= 0; --i) { adjustMinHeap(a, len, i); } } void adjustMinHeap(int a[], int len, int parentNodeIndex) { // 若只有一个元素,那么只能是堆顶元素,也没有必要再排序了 if (len <= 1) { return; } // 记录比父节点大的左孩子或者右孩子的索引 int targetIndex = -1; // 获取左、右孩子的索引 int leftChildIndex = 2 * parentNodeIndex + 1; int rightChildIndex = 2 * parentNodeIndex + 2; // 没有左孩子 if (leftChildIndex >= len) { return; } // 有左孩子,但是没有右孩子 if (rightChildIndex >= len) { targetIndex = leftChildIndex; } // 有左孩子和右孩子 else { // 取左、右孩子两者中最上的一个 targetIndex = a[leftChildIndex] < a[rightChildIndex] ? leftChildIndex : rightChildIndex; } // 只有孩子比父节点的值还要小,才需要交换 if (a[targetIndex] < a[parentNodeIndex]) { int temp = a[targetIndex]; a[targetIndex] = a[parentNodeIndex]; a[parentNodeIndex] = temp; // 交换完成后,有可能会导致a[targetIndex]结点所形成的子树不满足堆的条件, // 若不满足堆的条件,则调整之使之也成为堆 adjustMinHeap(a, len, targetIndex); } } void heapSort(int a[], int len) { if (len <= 1) { return; } // 初始堆成无序最小堆 initHeap(a, len); for (int i = len - 1; i > 0; --i) { // 将当前堆顶元素与最后一个元素交换,保证这一趟所查找到的堆顶元素与最后一个元素交换 // 注意:这里所说的最后不是a[len - 1],而是每一趟的范围中最后一个元素 // 为什么要加上>0判断?每次不是说堆顶一定是最小值吗?没错,每一趟调整后,堆顶是最小值的 // 但是,由于len的范围不断地缩小,导致某些特殊的序列出现异常 // 比如说,5, 3, 8, 6, 4序列,当调整i=1时,已经调整为3,4,5,6,8序列,已经有序了 // 但是导致了a[i]与a[0]交换,由于变成了4,3,5,6,8反而变成无序了! if (a[0] < a[i]) { int temp = a[0]; a[0] = a[i]; a[i] = temp; } // 范围变成为: // 0...len-1 // 0...len-1-1 // 0...1 // 结束 // 其中,0是堆顶,每次都是找出在指定的范围内比堆顶还小的元素,然后与堆顶元素交换 adjustMinHeap(a, i - 1, 0); } } |
(1)第一种方案:第3部分
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | /** * 算法君:一个专业的算法学习分享网站 * 算法君:专业分享--数据剖析--算法精解 * 算法君:http://www.suanfajun.com */ int main(int argc, char const *argv[]) { // int a[] = {5, 3, 8, 6, 4}; int a[] = {89,-7,999,-89,7,0,-888,7,-7}; heapSort(a, sizeof(a) / sizeof(int)); for (int i = 0; i < sizeof(a) / sizeof(int); ++i) { printf("%d \n", a[i]); } return 0; } |
(2)第二种方案
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 | /** * 算法君:一个专业的算法学习分享网站 * 算法君:专业分享--数据剖析--算法精解 * 算法君:http://www.suanfajun.com */ #include <stdio.h> #define NA -1 void swap(int *a,int *b)//该函数用于交换两个变量的值 { int temp=*a; *a=*b; *b=temp; } void HeapAdjust(int H[],int start,int end)//堆调整,将start和end之间的元素调整为最大堆 { int temp=H[start]; int parent=start,child; while(2*parent<=end) { child=2*parent; if(child!=end&&H[child]<H[child+1])++child; if(temp>H[child])break; else H[parent]=H[child]; parent=child; } H[parent]=temp; } void HeapSort(int H[],int L,int R) { for(int i=(R-L+1)/2;i>=L;--i)//调整整个二叉树为最大堆 HeapAdjust(H,i,R); for(int i=R;i>=L;--i) { swap(&H[L],&H[i]); HeapAdjust(H,L,i-1); } } int main(){ int A[]={NA,1,3,63,5,78,9,12,52,8};//从1开始存入数据 printf("Previous Arrary:"); for(int i=1;i<=9;++i) printf(" %d",A[i]); HeapSort(A,1,9); printf("\nSorted Arrary:"); for(int i=1;i<=9;++i) printf(" %d",A[i]); printf("\n"); return 0; } |
6.堆排序算法C++源代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 | /** * 算法君:一个专业的算法学习分享网站 * 算法君:专业分享--数据剖析--算法精解 * 算法君:http://www.suanfajun.com */ /*堆排序(大顶堆) 2017-04-22 20:04*/ #include <iostream> #include<algorithm> using namespace std; void HeapAdjust(int *a,int i,int size) //调整堆 { int lchild=2*i; //i的左孩子节点序号 int rchild=2*i+1; //i的右孩子节点序号 int max=i; //临时变量 if(i<=size/2) //如果i不是叶节点就不用进行调整 { if(lchild<=size&&a[lchild]>a[max]) { max=lchild; } if(rchild<=size&&a[rchild]>a[max]) { max=rchild; } if(max!=i) { swap(a[i],a[max]); HeapAdjust(a,max,size); //避免调整之后以max为父节点的子树不是堆 } } } void BuildHeap(int *a,int size) //建立堆 { int i; for(i=size/2;i>=1;i--) //非叶节点最大序号值为size/2 { HeapAdjust(a,i,size); } } void HeapSort(int *a,int size) //堆排序 { int i; BuildHeap(a,size); for(i=size;i>=1;i--) { //cout<<a[1]<<" "; swap(a[1],a[i]); //交换堆顶和最后一个元素,即每次将剩余元素中的最大者放到最后面 //BuildHeap(a,i-1); //将余下元素重新建立为大顶堆 HeapAdjust(a,1,i-1); //重新调整堆顶节点成为大顶堆 } } int main(int argc, char *argv[]) { //int a[]={0,16,20,3,11,17,8}; int a[100]; int size; while(scanf("%d",&size)==1&&size>0) { int i; for(i=1;i<=size;i++) cin>>a[i]; HeapSort(a,size); for(i=1;i<=size;i++) cout<<a[i]<<" "; cout<<endl; } return 0; } |

